Wie die Antworten auf Ihre ursprüngliche Frage bereits erläutert haben, benötigen Sie zusätzlichen Auftrieb, um nach oben zu beschleunigen. Sobald der Flügel in eine vertikale Bewegung versetzt ist, entspricht das Anheben jedoch wieder genau dem Gewicht, um den Flügel auf einer konstanten vertikalen Geschwindigkeit zu halten (wenn wir Schub und Widerstand für einen Moment vernachlässigen). Es ist kein zusätzlicher Auftrieb erforderlich, um diese vertikale Geschwindigkeit aufrechtzuerhalten. Nur wenn Sie weiter beschleunigen möchten, ist zusätzlicher Auftrieb erforderlich.

Die Erhöhung der potenziellen Energie kommt tatsächlich vom Propeller, da der Auftriebsvektor des Kletterflügels nach hinten geneigt ist

Schauen wir uns nun Ihr Experiment im Detail an: Ich gehe davon aus, dass der Flügel eine gewisse Masse hat, drehbar verriegelt ist und ohne diese Stange auf und ab gleitet Reibung. Wenn Sie das Auto beschleunigen, ist seine Geschwindigkeit irgendwann genau richtig, damit der Flügel genau den Auftrieb erzeugt, um sein eigenes Gewicht auszugleichen. Bei dieser Geschwindigkeit ist der Flügel an jeder Position entlang der Stange stabil. Wenn es ein wenig nach unten rutscht, erhöht sich sein Anstellwinkel $ \ alpha $ und erzeugt mehr Auftrieb, wodurch die Abwärtsbewegung gestoppt wird. Das Gegenteil gilt für jede Aufwärtsbewegung. Unten finden Sie eine Illustration des Prinzips. Der Cyan-Vektor ist die Vektorsumme des Flusses aufgrund von Vorwärtsbewegung (blau) und vertikaler Bewegung (rot), und dies wird der Flügel "bemerken".

Wenn das Auto weiter beschleunigt, erhöht sich der Auftrieb und wird jetzt größer als das Gewicht. Der Flügel beschleunigt nach oben, bis seine vertikale Geschwindigkeit seinen Anstellwinkel um genügend verringert, um die vertikalen aerodynamischen Kräfte so zu reduzieren, dass sie genau seinem Gewicht entsprechen. Jetzt haben Sie die gleiche Situation wie zuvor, jedoch nicht mit einer vertikalen Geschwindigkeit von Null, sondern mit einer positiven vertikalen Geschwindigkeit, die sicherstellt, dass der Flügel oben auf der Stange herausspringt, es sei denn, es gibt einen Stopp. Wenn der Flügel den Anschlag trifft, hört die vertikale Bewegung auf, der Anstellwinkel nimmt zu und der Flügel hebt nicht nur sich selbst, sondern auch einen Teil des Fahrzeuggewichts an.

Beachten Sie, dass ich jetzt von der Vertikalen gesprochen habe Komponenten der aerodynamischen Kräfte, nicht heben. Wenn Drag hinzugefügt wird, wird eine vertikale Komponente hinzugefügt, wenn der Flügel in Bewegung ist. Der Auftrieb ist definiert als die Summe der aerodynamischen Kräfte senkrecht zur Strömungsrichtung im Unendlichen und des parallelen Widerstands. Diese umständliche Definition stellt sicher, dass lokale Verzerrungen im Strömungsfeld die Richtung des Auftriebs und des Widerstands nicht beeinflussen. Die Auftriebsrichtung für den Kletterflügel zeigt leicht nach hinten und die Zugrichtung leicht nach unten. Dadurch wird der Summe der vertikalen aerodynamischen Kräfte eine gewisse Widerstandskomponente hinzugefügt, und der Auftrieb muss erhöht werden, um dies auszugleichen. Die horizontale Komponente des Auftriebs erhöht nun den Luftwiderstand und die Kräfte auf die Stange, sodass mehr Kraft vom Propeller benötigt wird, um den Kletterflügel durch die Luft zu drücken. Diese zusätzliche Kraft wird benötigt, um die potentielle Energie des Flügels auf seinem Weg nach oben zu erhöhen. Bei einem absteigenden Flügel ist das Gegenteil der Fall: Jetzt wird durch Ziehen eine vertikale Komponente hinzugefügt und der Auftrieb wird etwas langsamer. Die vordere Komponente des Auftriebs drückt nun gegen die Stange und verringert die Kraft, die der Propeller aufbringen muss. Die Verringerung der potentiellen Energie verringert nun die horizontalen aerodynamischen Kräfte.

Ein Flugzeug unterscheidet sich geringfügig, da es frei nach oben oder unten geneigt werden kann und der Schubwinkel mit ihm geneigt wird. Auf diese Weise kann der Pilot die Flugbahn und den Auftrieb auswählen, den der Flügel erzeugt. Die vertikale Bewegung stellt jedoch sicher, dass ein übermäßiger Auftrieb zu einer erhöhten vertikalen Geschwindigkeit und einem geringeren Anstellwinkel führt, sodass der übermäßige Auftrieb verschwindet. Bei einem Aufstieg muss der Schub größer sein als der Luftwiderstand, um die potenzielle Energie des Flugzeugs zu erhöhen. Jetzt trägt die vertikale Komponente des geneigten Schubvektors ein gewisses Gewicht, wodurch der zur Unterstützung des Gewichts erforderliche Auftrieb verringert wird.

Wenn Sie sagen,

Keine vom Propeller investierte Leistung fließt in die potenzielle Energie des Flügels. Der Aufstieg des Flügels erfolgt ausschließlich durch Heben.

Sie vermissen, woher die Energie des Flügels kommt. Lift ist keine magische Kraft, die aus dem Nichts potentielle Energie erzeugt: Sie wandelt nur die Fluggeschwindigkeit (kinetische Energie) in Höhe (potentielle Energie) um. In Ihrem Beispiel wird die vom Propeller investierte Leistung in kinetische Energie des gesamten Wagens einschließlich des Flügels umgewandelt. Auf diese Weise gelangt die Energie vom Propeller (oder seinem Kraftstoff) in die potenzielle Energie des Flügels. Sie müssen mehr Schub verwenden, um den Wagen mit angebrachtem Flügel anzutreiben, als wenn Sie den Flügel wegnehmen würden.

Es gibt zwei Möglichkeiten, die während eines Aufstiegs erzeugten Kräfte zu betrachten. Denken Sie daran, dass ein Flügel, der mehr Auftrieb erzeugt, auch mehr induzierten Widerstand erzeugt. Deshalb benötigen Sie übermäßigen Schub, um den übermäßigen Auftrieb zu erzeugen.

Für eine bestimmte Leistungseinstellung können Sie mit einer bestimmten Geschwindigkeit waagerecht fliegen. Wenn Sie sich neigen, erzeugen die Flügel einen übermäßigen Auftrieb, aber auch mehr Luftwiderstand. Obwohl ein Teil Ihres Schubes vertikal wirkt, gibt es keinen übermäßigen Schub, da der Luftwiderstand größer ist. Sie werden langsamer, der Lift wird kleiner und Sie werden aufhören zu klettern.

Stattdessen können Sie das Flugzeug gerade halten und mehr Schub hinzufügen. Dies erhöht Ihre Geschwindigkeit, was auch den Auftrieb von den Flügeln erhöht. Dies erhöht wiederum den induzierten Luftwiderstand, der schließlich den überschüssigen Schub bei einer neuen, höheren Fluggeschwindigkeit ausgleicht. Da Sie dadurch den Auftrieb erhöht haben, werden Sie klettern, obwohl Ihre Flügel eben sind. Sie können dies nur tun, weil Sie an erster Stelle mehr Leistung hinzugefügt haben.

(Ich fühle mich verpflichtet, darauf hinzuweisen, dass Sie normalerweise nicht so klettern würden: Um eine bessere Steiggeschwindigkeit zu erzielen, würden Sie im Allgemeinen Erhöhen Sie die Leistung und erhöhen Sie die Fluggeschwindigkeit, sodass Ihre Fluggeschwindigkeit auf die Geschwindigkeit sinkt, bei der die Flügel den größten Auftrieb bei geringstem Luftwiderstand erzeugen.)

Ich bin der Meinung, dass der Rest der Antworten unnötig komplex ist, wenn man bedenkt, wie einfach die Grundlagen hier sind:

Momentum

Frage: Ist es notwendig, dass L>m.g ( oder wie Sie sagen, ein Übermaß an Auftrieb), um zu klettern?

Antwort: Nein, zumindest kein anhaltender Überschuss an Auftrieb. Newtons Gesetze besagen, dass ein Objekt in Bewegung in diesem Zustand bleibt, es sei denn, eine Kraft wirkt auf es. Ein Kraftungleichgewicht ist erforderlich, um das Flugzeug in einen Aufstieg zu versetzen. Sobald dies erreicht ist, können die Kräfte ausgeglichen werden und das Flugzeug steigt weiter. Daher ist ein Übermaß an Auftrieb keine Bedingung, die ein Flugzeug benötigt, um einen Aufstieg aufrechtzuerhalten.

Energie

Frage: Ist es notwendig, dass wir dem System Energie hinzufügen (in der Form der Erhöhung unserer Leistungsabgabe), um zu klettern?

Antwort: Ja, wenn Energie gespart wird, müssen wir Energie hinzufügen, um an Höhe (und damit auch an Energie des Gravitationspotentials) zu gewinnen. Wir könnten keine Energie hinzufügen, die Leistung unserer Motoren nicht erhöhen und einfach hochziehen, die AoA erhöhen, aber auch den Luftwiderstand erhöhen, und wir würden für kurze Zeit klettern, wenn wir kinetische Energie gegen potentielle Gravitationsenergie tauschen, aber wir würden feststellen, dass unsere Das Flugzeug verlangsamt sich schnell und wir müssen unter unsere ursprüngliche Höhe tauchen, um zum Flug mit konstantem Niveau zurückzukehren.

Daher ist für den Aufstieg ein Leistungsüberschuss erforderlich, ein anhaltender Auftriebsüberschuss jedoch nicht.

Die einfache Antwort ist leicht zu demonstrieren. Starten Sie mit einem Flugzeug, das für Geradeaus- und Geradeausflug getrimmt ist. Zum Beispiel 1000 Fuß, 100 Meilen pro Stunde, 1500 U / min Stütze mit fester Steigung.

Auftrieb = Flugzeuggewicht und Schub = Flugzeugwiderstand.

Erhöhen Sie nun die Motordrehzahl um 150 U / min (10% mehr Schub), wodurch der Schub erhöht wird. Das Flugzeug beschleunigt für einen Moment, der erhöhte Luftstrom über dem Flügel und dem Stabilisator erhöht den Auftrieb und das Flugzeug gewinnt Höhe. In wenigen Sekunden gleicht sich das System wieder aus, die Fluggeschwindigkeit kehrt zu den getrimmten 100 Meilen pro Stunde zurück und der überschüssige Schub zeigt eine Steiggeschwindigkeit an. Das Flugzeug wird jetzt leicht angehoben, aber der Anstellwinkel bleibt konstant, da er durch die Trimmeinstellung des Stabilisators gesteuert wird, die wir nicht berührt haben.

Rollen Sie als Nächstes die Trimm des Aufzugs nach vorne, wodurch die Trimmung verringert wird Die Fluggeschwindigkeit wird leicht ansteigen und die Steiggeschwindigkeit wird sich verringern. Wenn die Steiggeschwindigkeit des Flugzeugs erneut auf geraden und ebenen Flug getrimmt wird, beträgt die Steiggeschwindigkeit 0, die Fluggeschwindigkeit liegt über 100 Meilen pro Stunde. Jetzt zeigt sich der zusätzliche Schub als erhöht an Drehzahl.

Um das Beispiel fortzusetzen, reduzieren Sie die Drehzahl wieder auf die ursprüngliche Drehzahl von 1500 U / min. Lassen Sie die Trimmung in Ruhe. Das Flugzeug sollte jetzt bei der neuen, etwas höheren Fluggeschwindigkeit eine anständige Geschwindigkeit anzeigen.

All dies wurde ohne Eingabe vom Steuerknüppel durchgeführt.

Jedes Mal, wenn der Pilot die primären Flugsteuerungen manövriert, gibt es einen fast sofortigen Handel zwischen Anstellwinkel, Geschwindigkeit, Auftrieb, Luftwiderstand, Trägheit, Steiggeschwindigkeit oder anständig. Jerry S.

Die obigen Antworten erklären die theoretische Lösung Ihres Problems auf wunderbare Weise, aber da Sie bis jetzt noch keine akzeptiert haben, würde ich die Lösung numerisch veranschaulichen.

  Lassen Sie uns Angenommen, Ihr Wagen bewegt sich mit einer konstanten Geschwindigkeit von 'v'Then, KE = 1/2 (mv ^ 2) D = 1/2 ((Dichte) (v ^ 2) S (Cd)) und Gesamtenergie E = K.E. + D * Abstand (unter der Annahme eines reibungslosen Zusammenspiels von Oberflächen überall) Cd = Cd0 + K (Cl) ^ 2distance = v * tso T.E. = 1/2 (v ^ 2) (m + (Dichte) SVt (Cd0 + K (Cl) ^ 2))  

Hier ist zu sehen, dass die Gesamtenergie für verwendet wird

1. Der kinetische Energieteil des Wagens
2. Der Auftriebskoeffizient des Wagenflügels

Der Auftriebskoeffizient ist daher verantwortlich für den Energieverbrauch3d beim Anheben des Flügels nach oben und daher gehorcht das gesamte System der Energieeinsparung

Aktualisierte Simulation ohne vertikale Widerstandskraft

In dieser Situation ist der Auftrieb beim Aufstieg nur für den Flügel größer als das Gewicht. Die vertikale Kraft stabilisiert sich, um dem Gewicht zu entsprechen, aber da der Auftriebsvektor aufgrund der Aufwärtsgeschwindigkeit leicht nach hinten geneigt ist, nimmt der aerodynamische Auftrieb zu.

Peter Kämpfs Antwort beschreibt, was in dieser Situation mit dem Flügel passiert, aber was Wir hatten keine Quantifizierung. Ich habe eine Echtzeitsimulation der Kräfte auf den Flügel in der Zeichnung des OP als Funktion der Fluggeschwindigkeit $ V_ {air} $ und der vertikalen Flügelgeschwindigkeit $ \ dot {z} $ durchgeführt. Die Kräfte auf den Flügel sind unten dargestellt. Ich habe ein NACA 0012-Profil mit einem $ \ alpha_0 $ von 2 Grad erstellt:

$$ L = lift = C_L \ cdot \ frac {1} {2} \ cdot \ rho \ cdot {V} ^ 2 \ cdot A \ tag {1} $$

$$ D = C_D \ cdot \ frac {1} {2} \ cdot \ rho \ cdot {V} ^ 2 \ cdot \ tag {2} A $$

Für NACA 0012 ist $ C_L $ proportional zu $ \ alpha $: $ C_L $ = 1 bei $ \ alpha $ = 10 Grad, daher $$ C_L = k_L \ cdot \ alpha \ tag {3} $$

Wenn der Flügel nach oben geht, der Winkel Anzahl der Angriffsänderungen: $$ \ Delta \ alpha = arctan (\ frac {\ dot {z}} {V_ {air}}) \ tag {4} $$

Wir fassen jetzt alle Konstanten zusammen : $ K_L = k_L \ cdot \ frac {1} {2} \ cdot \ rho \ cdot A $, $ K_D = 0,01 \ cdot \ frac {1} {2} \ cdot \ rho \ cdot A $ ($ C_D $ für Standardrauheit bei Re = 6 x $ 10 ^ 6 $ = 0,01 für Winkel bis zu 4 °)

Der Auftrieb dieses Anstellwinkels wird durch Kombinieren von (1), (3) und (4) ermittelt. :

$$ L = K_L \ cdot (\ alpha_0 - \ Delta \ alpha) \ cdot V ^ 2 \ tag {5} $$

Die resultierende Kraft $ F $ wird geteilt nach Masse zu Flügelbeschleunigung führen, die die ist n, das in einen digitalen Euler-Integrator integriert ist, um $ \ dot {z} $

L und D zu ergeben, sind mit dem freien Stromvektor V ausgerichtet, während das Gewicht immer mit der Vertikalen ausgerichtet ist. Wir nehmen den Cosinus des L-Vektors minus den Sinus des D-Vektors

$$ F_ {up} = L \ cdot cos (\ Delta \ alpha) - D \ cdot sin (\ Delta \ alpha) \ tag {6} $$ Nun zu:

• m = 1 kg
• A = 1 $ m ^ 2 $
• $ \ alpha_0 = 2 Grad $
• $ k_L $ = 0,1

Wir erhalten L = 9,81 N bei $ V_ {air} $ = 8,949 m / s. Wenn wir dann $ V_ {air} $ in 1,5 Sekunden von 8,949 auf 10,5 m / s erhöhen, erhält der Flügel eine anfängliche Beschleunigung nach oben. Nachdem die Beschleunigung 2,4 Sekunden Null ist, steigt der Flügel mit konstanter Geschwindigkeit $ \ dot {z} $ = 0,1 m / s an. Der Anstellwinkel hat sich dann von 2 ° auf 1,45 ° verringert.

Werte, die für den Beginn des Tests bis zu 3 Sekunden gedruckt wurden:

Es gibt einige Effekte 2. Ordnung in der Antwort, die auf digitale Instabilität aufgrund des großen Zeitschritts des Euler-Integrators zurückzuführen sind. Die Zeit, dies zu überprüfen, ist derzeit nicht verfügbar.

In der Endsituation beträgt L also 9,82 N, was aufgrund einer Erhöhung der Fluggeschwindigkeit größer ist als das Gewicht bei einem Aufstieg. Nicht viel - der Auftriebsvektor wird in einem kleinen Winkel nach hinten geneigt, der durch das Verhältnis von $ \ dot {z} $ und V bestimmt wird, das 0,01 beträgt. Die gesamte vertikale Kraft beträgt $ L \ cdot cos \ alpha - D \ cdot sin \ alpha - W $

Diese Frage enthält viel mehr, als man auf den ersten Blick sieht - es ist eine ziemlich interessante Frage.

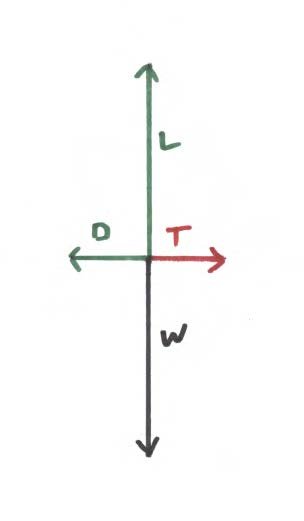
Normalerweise wirkt der Schubvektor im Kontext des Starrflügelfluges ungefähr parallel zu die Flugbahn durch die Luftmasse. Wenn der Schubvektor genau parallel zur Flugbahn durch die Luftmasse ist und die Flugbahn linear ist, anstatt sich nach oben oder unten oder zu beiden Seiten zu krümmen, sieht das Vektordiagramm der Kräfte beim Aufstieg folgendermaßen aus (linker Fall) Steigwinkel von 45 Grad - rechter Fall - Steigwinkel von 90 Grad):

Angetriebener Aufstieg bei Steigwinkeln von 45 und 90 Grad:

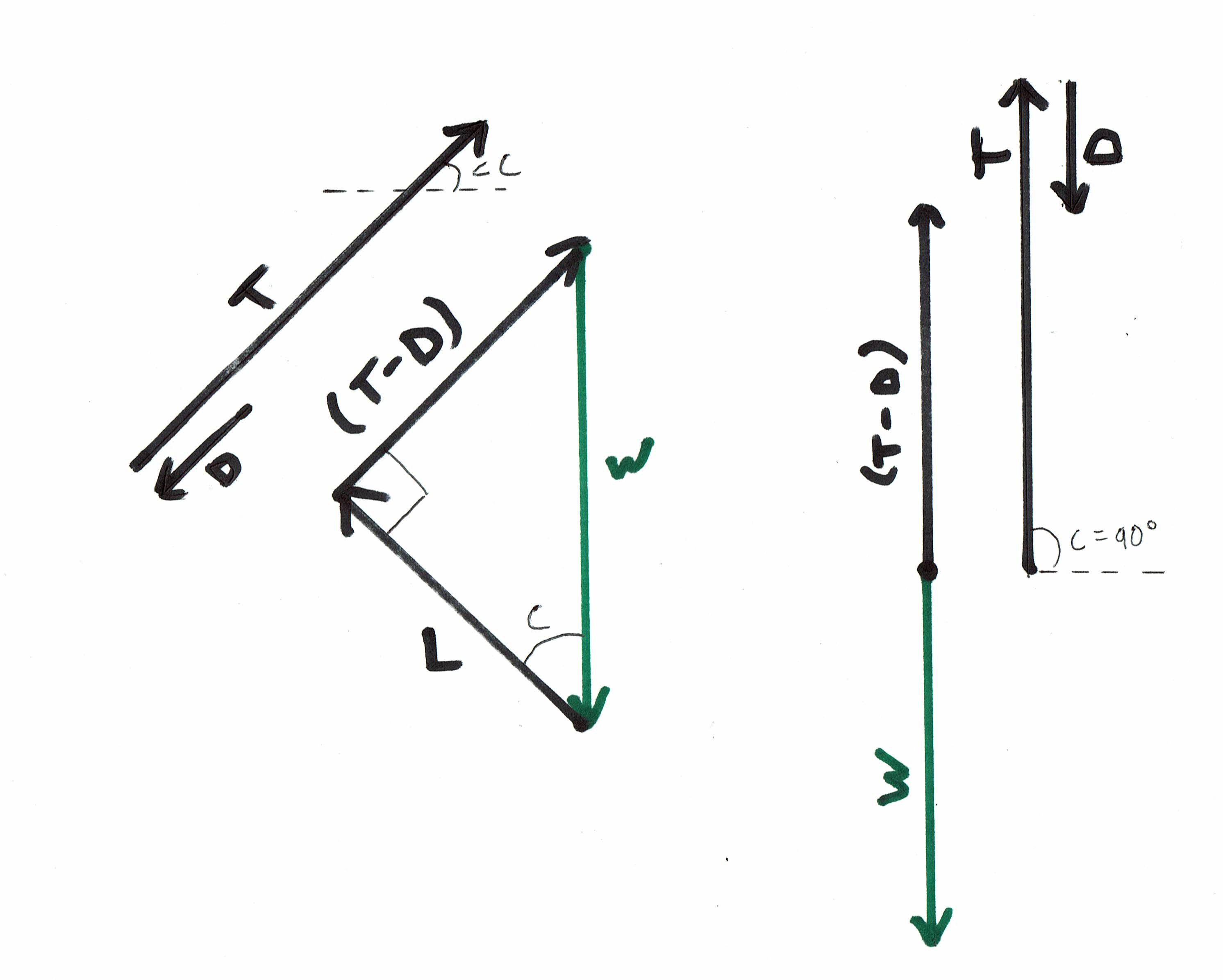
Wir können sehen, dass Lift = Weight * Cosine (Steigwinkel). Im linken Diagramm beträgt der Steigwinkel 45 Grad und Lift = 0,707 * Gewicht. Im rechten Diagramm beträgt der Steigwinkel 90 Grad und der Auftrieb Null.

In diesen Diagrammen wird jedoch davon ausgegangen, dass der Schubvektor parallel zur Flugbahn durch die Luftmasse wirkt. Wenn dies nicht zutrifft, gilt natürlich auch nicht mehr die Schubgleichung Lift = Gewicht * Kosinus (Steigwinkel). Um einen Extremfall zu nehmen, beachten Sie, dass der Flügel "entladen" wird, wenn die Auspuffdüsen eines Harrier "Sprungstrahls" gerade nach unten zeigen - das Flugzeug kann mit einer Fluggeschwindigkeit von Null und einem Hub von Null schweben, der vollständig durch Schub unterstützt wird. Umgekehrt zieht die Schleppleine während eines Segelflugwindenstarts am Segelflugzeug steil nach unten. Auch dies kann als eine Form des "vektorisierten Schubes" angesehen werden - aber jetzt wird die Belastung des Flügels eher erhöht als verringert, sodass die Flügel eine Auftriebskraft erzeugen müssen, die viel größer als das Gewicht des Flugzeugs ist.

In dem in dieser Frage dargestellten Fall wirkt Thrust NICHT entlang der Flugbahn des "Flugzeugs", wenn wir den Flügel als "Flugzeug" betrachten. Wenn der Flügel den Pol hinaufsteigt, bewirkt die vertikale Bewegung eine Änderung der Flugbahnrichtung des Flügels durch die Luftmasse und auch eine Änderung der Richtung des "relativen Windes", es gibt jedoch keine entsprechende Änderung der Richtung des Schubvektor. Somit ist das in der Frage vorgestellte Gedankenexperiment NICHT repräsentativ für die typische Situation im Starrflügelflug. Der Schubvektor ist NICHT in der Richtung relativ zur Sehnenlinie des Flügels festgelegt und wirkt NICHT ungefähr parallel zur Richtung des "relativen Windes", den der Flügel erfährt, und zur Richtung der Flugbahn des Flügels durch die Luftmasse.

Außerdem fehlt der grundlegende Mechanismus, der die Fluggeschwindigkeit eines Starrflügelflugzeugs regelt. Normalerweise krümmt sich die Flugbahn beim Steigen eines Flugzeugs nach oben, wenn der Auftrieb das Gewicht überschreitet, wodurch der Gewichtsvektor eine größere Komponente aufweist, die parallel zur Flugbahnrichtung des Flugzeugs durch die Luftmasse wirkt, was zu einer Verringerung der Geschwindigkeit führt. Da in diesem Experiment der Flügel in Längsrichtung auf dem Wagen "verriegelt" ist, scheint es, dass der Wagen, wenn sich die Flugbahn des Flügels nach oben krümmt, so viel Schub liefert, wie zum Halten der horizontalen Komponente erforderlich ist der Geschwindigkeitsvektorkomponente des Flügels genau konstant. Angenommen, der Luftwiderstand des Flügels ist im Vergleich zum Luftwiderstand aus anderen Quellen wie Radwiderstand und Radlagerwiderstand des Wagens trivial, so dass Schwankungen des Luftwiderstands des Flügels im Wesentlichen keinen Einfluss auf die Fluggeschwindigkeit und die Bodengeschwindigkeit des Wagens haben.

Die Kräfte, die in diesem Gedankenexperiment auf den Flügel wirken, unterscheiden sich also stark von den Kräften, die normalerweise im tatsächlichen Flug auf ein Starrflügelflugzeug wirken. Es sollte nicht überraschen, dass bei diesem Gedankenexperiment der Auftrieb tatsächlich größer als das Gewicht sein muss, damit der Flügel auf die Stange klettern kann.

Wir könnten diese Antwort hier wirklich beenden. Es ist jedoch ziemlich interessant, die Kräfte, die im Gedankenexperiment auf den Flügel wirken, etwas genauer zu betrachten.

Was sind einige der bemerkenswerten Merkmale des Gedankenexperiments?

Wie wir bereits bemerkt haben, ist der Flügel in Bezug auf den Wagen vorne und hinten verriegelt Richtung. Der Flügel kann in Längsrichtung relativ zum Wagen nicht beschleunigen oder verlangsamen. Wenn der Luftwiderstand vom Flügel im Vergleich zu den anderen auf den Wagen einwirkenden Luftwiderstandsquellen geringer ist, so dass der Luftwiderstand vom Flügel im Wesentlichen keinen Einfluss auf die Fluggeschwindigkeit des Wagens hat, bedeutet dies, dass der Flügel nicht beschleunigen oder verlangsamen kann die Längsrichtung relativ zur Luftmasse (oder relativ zum Boden). Der Wagen überträgt auf den Flügel, jedoch ist viel Schub erforderlich, um die Längskomponente des Fluggeschwindigkeitsvektors des Flügels konstant zu halten. Dies unterscheidet sich stark von der typischen Situation im Starrflügelflug.

Auch. Da das Gedankenexperiment ursprünglich formuliert wurde, ist der Flügel in einer konstanten Nicklage verriegelt.

Hier ist ein Vektordiagramm, das die Situation veranschaulicht, in der sich der Wagen mit einer konstanten Fluggeschwindigkeit bewegt, die NICHT hoch genug ist, um die Flügel zum Abheben vom Wagen:

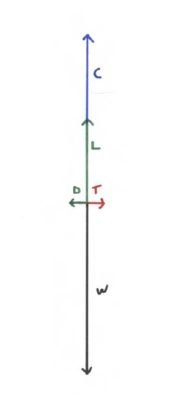
Die dargestellten Kräfte umfassen Heben (L), Ziehen (D), Gewicht (W), Schub (T) und die Aufwärtskraft (C), die der Wagen auf den Flügel ausübt, wenn der Flügel auf dem Wagen ruht. Die Nettokraft ist Null. Das L / D-Verhältnis beträgt 10: 1.

Nehmen wir nun an, wir halten den Flügel mit einem Riegel gedrückt, während wir die Leistung erhöhen und auf eine höhere Fluggeschwindigkeit beschleunigen, und lassen dann alles stabilisieren. Dann entriegeln wir den Haken. Das folgende Diagramm zeigt die Situation in dem Moment, in dem wir den Haken entriegeln -

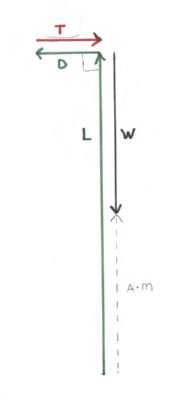
Der Flügel hat noch nicht begonnen, sich nach oben zu heben Es gibt keine Änderung in der Richtung der Flugbahn des Flügels durch die Luftmasse oder in der Richtung der Auftriebs- und Widerstandsvektoren. Der Anstellwinkel des Flügels hat sich nicht geändert, daher haben sich die Auftriebs- und Widerstandskoeffizienten nicht geändert, sodass das L / D-Verhältnis immer noch 10/1 beträgt. Die gestrichelte Linie stellt den Nettokraftvektor dar, der einfach die Vektorsumme aller anderen Kraftvektoren ist. Beschleunigung = Kraft / Masse, daher können wir den Nettokraftvektor auch als "Beschleunigung * Masse" bezeichnen.

Was passiert, wenn der Flügel die Stange hinauf steigt (beschleunigt)? Die Aufwärtsgeschwindigkeit des Flügels bewirkt eine Änderung des "relativen Windes", den der Flügel erfährt. Der Anstellwinkel des Flügels nimmt sofort ab oder wird negativ, sodass der Auftriebskoeffizient abnimmt und das L / D-Verhältnis abnimmt. (Der Luftwiderstandsbeiwert kann ebenfalls abnehmen, jedoch nicht so stark wie der Auftriebskoeffizient.) Wenn der Flügel ein gewölbtes, nicht symmetrisches Tragflächenprofil aufweist, erzeugt er immer noch Auftrieb bei einem kleinen negativen Anstellwinkel, jedoch nicht sehr stark. - Der Auftriebskoeffizient ist niedrig. Wenn der Flügel eine bestimmte vertikale Aufwärtsgeschwindigkeit erreicht, hat sich der Auftrieb so weit verringert, dass die vertikale Komponente der auf den Flügel wirkenden aerodynamischen Nettokraft nicht länger größer als das Gewicht ist und die Nettokraft auf den Flügel auf Null abfällt. und der Flügel kann nicht mehr beschleunigen, sondern bewegt sich mit konstanter Vertikalgeschwindigkeit den Pol hinauf. Die folgende Abbildung zeigt diese Situation:

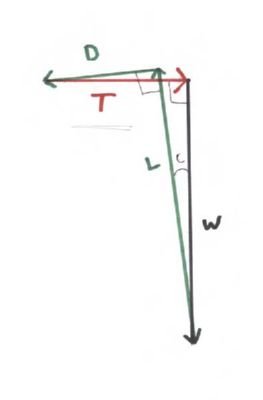
Die Richtung des Flügels durch die Luftmasse ist parallel (und entgegengesetzt zu) der Richtung des Widerstandsvektors. Der Steigwinkel - im Diagramm mit "C" bezeichnet - ist der spitze Winkel, der zwischen den Schub- und Widerstandsvektoren sowie zwischen den Auftriebs- und Gewichtsvektoren gebildet wird. Dies ist auch der Winkel zwischen dem Drag-Vektor und dem Horizont sowie der Winkel zwischen dem Lift-Vektor und der vertikalen Richtung. Die Vektoren können alle von Kopf bis Schwanz in einer geschlossenen Figur angeordnet sein, so dass die Nettokraft Null ist. Der Auftrieb ist etwas größer als das Gewicht und der Schub ist etwas größer als der Widerstand. Wenn der Flügel ohne Einfall auf dem Wagen montiert ist, muss der Anstellwinkel des Flügels leicht negativ sein - tatsächlich muss er negativen "C" Grad entsprechen. Wir haben das L / D-Verhältnis als 2/1 gezeichnet, um die Abnahme des Auftriebskoeffizienten des Flügels darzustellen, die durch die Änderung des Anstellwinkels verursacht wird. Der Flügel bewegt sich mit konstanter Geschwindigkeit den Pol hinauf.

Interessanterweise ist diese Situation praktisch identisch mit der Situation des aufsteigenden Flügels, wenn ein Flugzeug in einen steileren Querneigungswinkel rollt, insbesondere wenn die Rolle von einem Spoiler angetrieben wird, der auf dem absteigenden Flügel ohne Änderung an eingesetzt ist die Form des aufsteigenden Flügels. Die Änderung des Anstellwinkels, die durch die aufsteigende Bewegung des Flügels durch die Luftmasse verursacht wird, begrenzt die vertikale Geschwindigkeit, die der aufsteigende Flügel erreichen kann - dies wird als "Rolldämpfung" bezeichnet. Die Auftriebs- und Widerstandsvektoren sind aus der Richtung, in die sie vor Beginn der Rollbewegung gezeigt haben, "nach hinten gedreht" oder "nach hinten gedreht". Sie können diese "Drehung" auch in diesem Diagramm sehen https: //www.av8n. com / how / img48 / nachteilig-gieren-stetig.png aus diesem Abschnitt https://www.av8n.com/how/htm/yaw.html#sec-adverse-yaw der ausgezeichneten "See How It Flies" -Website https://www.av8n.com/how/.

Die Situation ist auch genau so, wie wir es hätten, wenn wir ein Segelflugzeug unter den folgenden Bedingungen ziehen würden: 1) Wir haben ein sehr langes Abschleppseil - so lang, dass der Winkel des Abschleppseils relativ zum Horizont wird überhaupt nicht von der Steiggeschwindigkeit des Segelflugzeugs relativ zum Schleppflugzeug beeinflusst. 2) Das Schleppflugzeug fliegt in eine solche Richtung, dass das Seilende des Segelflugzeugs genau horizontal am Segelflugzeug zieht. 3) Der Luftwiderstand des Segelflugzeugs ist im Vergleich zu Schub und Luftwiderstand des Schleppflugzeugs trivial, sodass die aerodynamische Situation des Segelflugzeugs keinen Einfluss auf das Schleppflugzeug hat Fluggeschwindigkeit. 4) Der Segelflugzeugpilot gibt Pitch-Steuereingaben so ein, dass die Pitch-Haltung des Segelflugzeugs unabhängig von der Steiggeschwindigkeit relativ zum Horizont konstant bleibt.

Was ist nun, wenn wir das Experiment modifizieren, indem wir zulassen, dass die Nicklage des Flügels variiert, während der Anstellwinkel des Flügels relativ zur Flugbahn des Flügels durch die Luftmasse konstant gehalten wird - möglicherweise durch Hinzufügen einer Stabilisierungsschaufel oder Schwanz zur Rückseite des Flügels?

Was passiert nun, wenn der Flügel anfängt zu steigen?

Die folgende Abbildung zeigt eine Situation, in der der Auftrieb genau dem Gewicht entspricht. Der Widerstandsvektor ist horizontal, sodass der Flügel nicht durch die Luft steigen oder fallen kann - er muss in einer festen Position auf der Stange bleiben.

Beachten Sie, dass wir uns entschieden haben, ein 5: 1 L / D-Verhältnis für diese Version des Gedankenexperiments zu veranschaulichen.

Was ist nun, wenn wir dem Flügel den kleinsten Aufwärtsschub geben, damit er anfängt zu steigen? Sobald es zu steigen beginnt, wird seine Geschwindigkeit durch die Luftmasse durch seine vertikale Bewegung erhöht. Und jetzt kann sich der Flügel frei drehen, so dass sein Anstellwinkel konstant bleiben kann, sodass wir nicht den "Dämpfungseffekt" haben, den wir in der früheren Version des Experiments hatten. Die daraus resultierende Erhöhung der Fluggeschwindigkeit und des Auftriebs ähnelt der eines Segelflugzeugs, das sich auf einem Windenschleppwagen erhebt, mit der Ausnahme, dass beim Flügel des imaginären Wagens der Schubvektor horizontal bleibt und nicht teilweise nach unten zeigt. Der Steigwinkel des Flügels durch die Luftmasse wird mit zunehmender vertikaler Geschwindigkeit immer steiler. Dadurch erhöht sich die Fluggeschwindigkeit, wodurch der Auftriebsvektor größer wird.

Die folgende Abbildung zeigt die Situation, die wir sehen, wenn der Steigwinkel des Flügels durch die Luftmasse 60 Grad erreicht. Wiederum repräsentiert die gestrichelte Linie den Nettokraftvektor, der einfach die Vektorsumme aller anderen Kraftvektoren ist. Beschleunigung = Kraft / Masse, daher können wir den Nettokraftvektor auch als "Beschleunigung * Masse" bezeichnen.

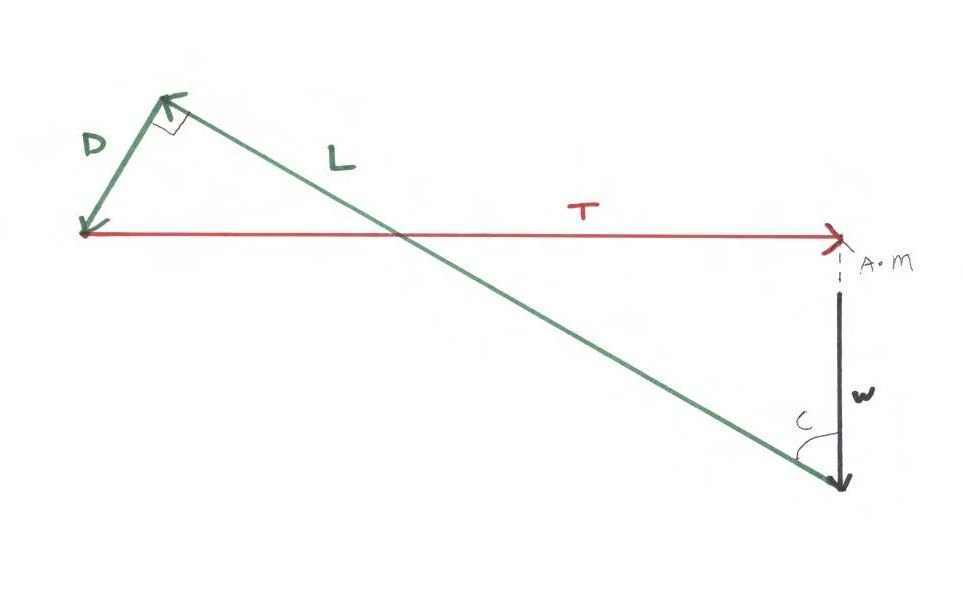
In diesem speziellen Fall Wir haben die Auftriebs- und Gewichtsvektoren so dimensioniert, dass sie die Situation darstellen, in der die horizontale Komponente der Geschwindigkeit des Flügels durch die Luftmasse genau dieselbe ist wie im vorherigen Diagramm oben, in der der Auftrieb genau dem Gewicht in dem Fall entsprach, in dem die Die Flugbahn des Flügels war horizontal. Durch einfaches Aufsteigen hat der Flügel eine Verdoppelung der Fluggeschwindigkeit und eine Vervierfachung der Größe des Auftriebsvektors erfahren. Die Summe der vertikalen Komponenten der Auftriebs- und Widerstandsvektoren beträgt nun das 1,3-fache des Flügelgewichts. Natürlich könnten wir das Diagramm so modifizieren, dass es einen Fall darstellt, in dem der Flügel eine Nettokraft nach oben erfährt, noch bevor er nach oben beschleunigt, indem wir einfach die Größe des Gewichtsvektors relativ zu den anderen Vektoren verringern.

Wenn die Geschwindigkeit des Wagens konstant bleibt und der Wagen so viel Schub auf den Flügel übertragen kann, dass er in Längsrichtung relativ zum Wagen an Ort und Stelle bleibt, beschleunigt der Flügel weiter und schneller schneller auf der Stange?

Es stellt sich heraus, dass dies nicht der Fall ist. Selbst wenn der Flügel überhaupt kein Gewicht hat, hört er auf, nach oben zu beschleunigen, sobald sein Steigwinkel der inversen Tangente des L / D-Verhältnisses entspricht. Für den hier dargestellten 5/1-Fall beträgt dieser Steigwinkel 78,7 Grad. Wenn der Flügel Gewicht hat, ist der maximal erreichbare Steigwinkel geringer. In dem oben dargestellten speziellen Fall, in dem der Gewichtsvektor genau gleich dem Auftriebsvektor ist, der existierte, als der Flügel eine Aufwärtsgeschwindigkeit von Null hatte, liegt der maximal erreichbare Steigwinkel irgendwo zwischen 70 und 75 Grad. Oberhalb dieses maximal erreichbaren Steigwinkels addieren sich die vertikalen Komponenten von Heben und Ziehen nicht mehr zu einem Wert, der größer als das Gewicht ist. Selbst wenn der Flügel frei schwenkbar ist, um einen konstanten Anstellwinkel aufrechtzuerhalten, und der Wagen über einen unendlichen Schub verfügt, um trotz Änderungen der Widerstandskraft des Flügels eine konstante Fluggeschwindigkeit aufrechtzuerhalten, gibt es eine Grenze für die Steigwinkel, den der Flügel erreichen kann.

Hier ist eine interessante Tabelle

ca-cos-sin-aspd-L-D-vcL-vcD-net aero vc-net vert

0 1,00 0,00 1,00 1,00 .200 1,00 0,00 1,00 0,00

30,866,600 1,15 1,33,267 1,15,133 1,02,021

45,707,707 1,41 2,00 .400 1,41 .283 1,13 0,13

60 .500 .866 2,00 4,00 .800 2,00 .693 1,31 0,31

70 .342 .940 2,92 8,55 1,71 2,92 1,61 1,32 0,32

75 .259 .966 3.86 14.9 2.99 3.86 2.88 .980 -0.02

80 .174 .985 5.76 33.2 6.63 5.76 6.53 -.773 -1.773

Annahmen -

ca = Steigwinkel in Grad

cos = Kosinus des Steigwinkels

sin = Sinus des Steigwinkels

airspd = Geschwindigkeit des Flügels durch die Luft in beliebigen Einheiten

L = Heben in beliebigen Einheiten

D = Ziehen Sie in denselben Einheiten wie L

Wir haben ein L / D-Verhältnis von 5/1

vcL = vertikale Komponente des Auftriebs (wirkt nach oben) = L * Cosinus (Steigwinkel)

vcD = vertikale Komponente von gewählt Luftwiderstand (wirkt nach unten) = D * Sinus (Steigwinkel)

net aero vc = vertikale Komponente der aerodynamischen Nettokraft = (vcL-vcD) - ein positives Vorzeichen bedeutet, dass die aerodynamische Nettokraft nach oben wirkt, während ein negatives Vorzeichen bedeutet, dass die aerodynamische Nettokraft nach unten wirkt.

net vert = net vertikale Kraft = (net aero vc - Gewicht), unter der Annahme, dass das Gewicht so gewählt wird, dass das Gewicht genau gleich ist der Wert des Auftriebsvektors in dem Fall, in dem der Steigwinkel Null ist.

Wenn die letzte Spalte (net vert) negativ ist, bedeutet dies, dass in dem Fall, in dem das Gewicht auf den beschriebenen bestimmten Wert eingestellt ist oben muss sich die Steiggeschwindigkeit verlangsamen (und der Steigwinkel muss sich verringern).

Wenn die vorletzte Spalte negativ ist, muss sich die Steiggeschwindigkeit verlangsamen (und der Steigwinkel muss sich verringern), selbst wenn das Gewicht ist Null.

Diese Version des Gedankenexperiments - bei der die Nicklage des Flügels frei variiert werden kann, um einen konstanten Anstellwinkel aufrechtzuerhalten - ähnelt in etwa dem, was zu Beginn des Segelflugzeugs der Segelflugzeugwinde geschieht. Besonders in der Nähe des Schleppanfangs, wenn die Schleppleine sehr lang ist und die Schleppkraft eine Weile fast horizontal bleibt, selbst wenn das Segelflugzeug schnell zu steigen beginnt.

Schließlich enthielt die ursprüngliche Frage die folgende Zeile: "Bitte beachten Sie, dass - da der Schub horizontal ist - die verbrannte chemische Energie in die kinetische Energie des Wagens und / oder in die Wärmeenergie (aufgrund der Überwindung des Luftwiderstands) fließt. Es wird keine Energie investiert durch den Propeller geht in potentielle Energie des Flügels über, der Aufstieg des Flügels erfolgt rein durch Auftrieb. " Der Schub funktioniert sicherlich entlang der Flugbahnrichtung durch die Luftmasse, die niemals rein vertikal ist. Die Situation scheint analog zu einem leichten Würfel (z. B. aus Balsaholz) zu sein, der von einem horizontal wehenden Wind auf eine rutschige Rampe gesprengt wird. Erhöht der Wind die potentielle Energie des Würfels?

Weitere Informationen zur "konventionelleren" Klettersituation - einem Starrflügelflugzeug mit parallel zur Flugbahnrichtung wirkendem Schub - finden Sie in den entsprechenden Antworten auf verwandte Fragen:

: Hebt das Heben bei einem Aufstieg das gleiche Gewicht? "

" Was erzeugt in einem Segelflugzeug Schub entlang der Fluglinie? "

"Gravitationsleistung vs. Motorleistung"

"Der Abstieg auf einer bestimmten Gleitneigung (z. B. ILS) bei einer bestimmten Fluggeschwindigkeit ist die Größe des Auftriebsvektors bei Gegenwind und Rückenwind unterschiedlich? "

" Ändern wir den Anstellwinkel durch Ändern der Steigung eines Flugzeugs? "

Die andere Antwort (und die Grundvoraussetzung) sind irreführend. Die Luftfahrt ist eine sorgfältige Balance von fast allem, und Sie erhalten selten mehr von einem, ohne etwas von dem anderen zu verlieren.

Betrachten Sie eine Rakete. Keine Flügel und damit kein Auftrieb. Meeresspiegel, 0 m / s bis zur Umlaufbahn in 8 Minuten. Alles mit einer ziemlich lächerlichen Menge an Kraft.

Betrachten Sie nun ein Luftschiff. Auch keine Flügel, aber übermäßiger Auftrieb. Geht ganz von alleine hoch. Die Triebwerke dienen nur zum Manövrieren. Wenn Sie sie entfernen, nennen wir das Ding normalerweise einen Ballon.

Eines der lächerlichsten Dinge, die ich je gehört habe, war ein Fluglehrer, der behauptete, dass der Gashebel die Höhe und der Aufzug die Höhe steuert Geschwindigkeit. Ich rief die komplette BS in der Erklärung an und fragte, ob er lieber auf einen Cumulo-Granitus zusteuern würde, würde er es vorziehen, die Kontrollen zu verstärken oder ziemlich scharf zurückzureißen?

Was er zu vermitteln versuchte, war das Im extrem engen Bereich des Geradeaus- und Horizontalfluges * wirkt sich die Einstellung der Leistung auf die Geschwindigkeit aus, die sich auf den Auftrieb auswirkt, und das Flugzeug stabilisiert sich nach einer Leistungsanpassung schließlich in einer anderen Höhe. Durch Anpassen der Tonhöhe wird Ihre Geschwindigkeit fast sofort geändert, aber auch Ihre Höhe. Sie könnten eine Demonstration der gleichzeitigen Einstellung von Leistung und Tonhöhe arrangieren und nichts anderes ändern, aber das beweist im Grunde meinen Standpunkt. Wenn Sie langsamer fahren möchten (z. B. landen), lassen Sie den Gashebel voll und ziehen Sie den Steuerknüppel ganz zurück? Natürlich nicht. Es ist eine sehr heikle Balance, und Piloten verbringen viel Zeit mit Lernen. Oder wenn Sie für bestimmte asiatische Fluggesellschaften arbeiten, haben Sie nur einige sehr teure Computer, die das für Sie erledigen.

• Ja, wir verbringen viel Zeit dort, aber überlegen Sie, wie genau Sie sein müssen. Ein unkorrigierter Bruchteil eines Grades in einer beliebigen Achse führt dazu, dass Sie abstürzen, bevor Ihnen der Kraftstoff ausgeht.